absolute, relative und prozentuale Häufigkeiten 

Inhalt
  1 Einführung
  2 Verwendung in Statistik I
  3 Symbole und Berechnung
    3.1 Symbole
    3.2 Berechnung
  4 Beispiel
    4.1 tabellarische Darstellung
    4.2 grafhische Darstellung

1 Einführung

Die Anzahl der Beobachtungen einer bestimmten Merkmalsausprägung wird in der Statistik als Häufigkeit bezeichnet. In den meisten Fällen liegen die statistischen Daten in absoluten Häufigkeiten (engl. frequencies) vor. So haben z.B. 25 von 100 Familien ein Einkommen von 3000-4000 DM pro Monat, 6 von 10 Personen sind der Meinung, daß mehr Geld für soziale Zwecke ausgegeben werden sollte etc.

Einige Berechnungen in der Statistik I können diese absoluten Daten jedoch nicht verwenden, sondern benötigen relative oder prozentuale Werte. Um die Berechnung und den Einsatz dieser Werte soll es hier gehen.

2 Verwendung in Statistik I

Absolute Häufigkeiten werden z.B. benutzt bei der Berechnung des arithmetischen Mittels und des feinberechneten Medians, dem Chi-Quadrat oder der Regression.

Relative und prozentuale Werte erlauben ebenfalls einen besseren Vergleich mehrerer Verteilungen, in denen die Anzahl der befragten Probanden N nicht gleich ist. Ebenso können diese Daten grafisch dargestellt werden.

Relative und prozentuale Daten finden ihre Anwendung vornehmlich beim Gini-Koeffizient und der Lorenz-Kurve.

3 Symbole und Berechnung

3.1 Symbole

absolute Häufigkeit:
relative Häufigkeit:
prozentuale Häufigkeit:

3.2 Berechnung

Ausgehend von absoluten Werten können relative und prozentuale Häufigkeiten sehr einfach berechnet werden:

		darf 1 nie übersteigen
		darf 100% nie übersteigen

4 Beispiel

In einem Unternehmen mit N=92 Beschäftigten wurde die Anzahl der Kinder pro Mitarbeiter ermittlet.

4.1 tabellarische Darstellung

4.2 graphische Darstellung

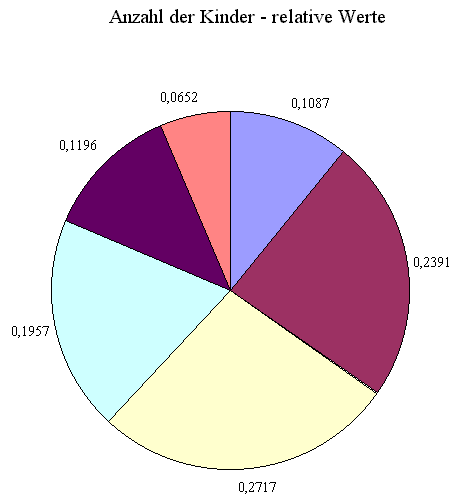
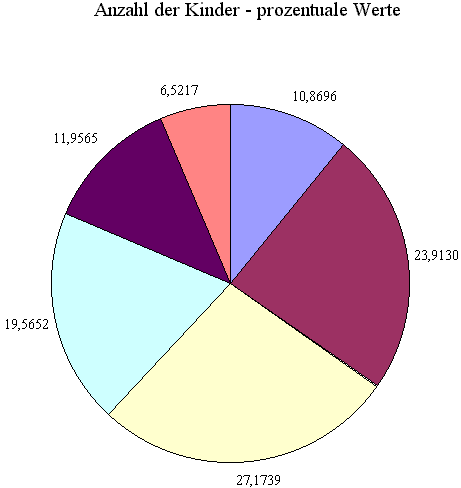
In der Legende ist die Anzahl der Kinder festgehalten. Der blaue Bereich in den Kreisdiagrammen bedeutet also kein Kind. Die Häufigkeit der Ausprägungen steht bei den jeweiligen Segmenten.

Wie ersichtlich, sind die prozentualen Angaben wesentlich griffiger als die relativen. An der Größe der Segmente ändert sich logischerweise nichts.