Wie bereits angesprochen sagt die Regressionsfunktion für sich noch nichts darüber aus, wie stark der statistische Zusammenhang zweier Variablen tatsächlich ist. Eine Regressionsgerade läßt sich auch berechnen, wenn so gut wie kein Zusammenhang vorliegt.
Graphisch läßt sich die Stärke des Zusammenhanges daran einschätzen, wie eng oder weit die Punktwolke um die Regressionsgerade streut.
Eine der gebräuchlichsten Maßzahlen, um für metrische Daten die Stärke des Zusammenhanges zu ermitteln ist der Korrelationskoeffizient r nach Bravais-Pearson.
Er ist definiert als:
![]()
Für die Berechnung von Hand verwendet man die Umformungen
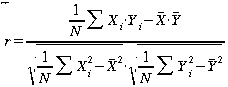 für
Einzelwerte, und
für
Einzelwerte, und
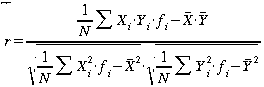 für
gruppierte Daten.
für
gruppierte Daten.
Es gilt:
![]() ,
wobei -1 einem vollständigen negativen, 0 statistischer
Unabhängigkeit und +1 einem vollständigen positiven
Zusammenhang entspricht.
,
wobei -1 einem vollständigen negativen, 0 statistischer
Unabhängigkeit und +1 einem vollständigen positiven
Zusammenhang entspricht.
![]() Beachten Sie bei der Berechnung von Hand:
Beachten Sie bei der Berechnung von Hand:
Der Zähler
der Berechnungsformel für b ist identisch mit dem Zähler
des Korrelationskoeffizienten r. Da man in der Regel die
Regressionsfunktion schon berechnet hat, kann er einfach übernommen
werden. Im Nenner steht das Produkt der beiden Standardabweichungen.
Zwischen b und r besteht daher folgende Beziehung:
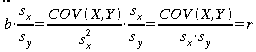 ,
d.h. wir können r auch berechnen als:
,
d.h. wir können r auch berechnen als:
![]()
Für die Berechnung der Regressionsgeraden und des Korrelationskoeffizienten benötigen Sie eine Arbeitstabelle mit den Spalten:
|
Xi |
Yi |
XiYi |
|
|
Das Konzept des Determinationskoeffizienten beruht auf dem Prinzip der Varianzzerlegung.
Sollte man ohne Information über die unabhängige
Variable eine Prognose für die abhängige Variable abgeben,
so könnte die nur lauten:
![]() ,
das arithmetische Mittel von Y. Mit Hilfe der Regressionsfunktion
,
das arithmetische Mittel von Y. Mit Hilfe der Regressionsfunktion
![]() ,
welche die Merkmalsausprägungen von Y als Funktion von X
beschreibt, können wir erklären, weshalb für ein
bestimmtes Xi Y nicht den Wert
,
welche die Merkmalsausprägungen von Y als Funktion von X
beschreibt, können wir erklären, weshalb für ein
bestimmtes Xi Y nicht den Wert
![]() annimmt, sondern
annimmt, sondern
![]() ,
den entsprechenden Wert der Regressionsfunktion. Diese Abweichung vom
Mittelwert ist durch die Abhängigkeit von X erklärt. Man
spricht von der erklärten Varianz. Liegt der für Xi
vorgefundene empirische Wert jedoch nicht auf der Regressionsgeraden,
so liegt eine weitere Abweichung vor, die nicht durch die
Regressionsfunktion erklärt werden kann - die nicht erklärte
Varianz bzw. der Fehler
,
den entsprechenden Wert der Regressionsfunktion. Diese Abweichung vom
Mittelwert ist durch die Abhängigkeit von X erklärt. Man
spricht von der erklärten Varianz. Liegt der für Xi
vorgefundene empirische Wert jedoch nicht auf der Regressionsgeraden,
so liegt eine weitere Abweichung vor, die nicht durch die
Regressionsfunktion erklärt werden kann - die nicht erklärte
Varianz bzw. der Fehler
![]() .
Dieser Fehler ist in der Regel auf weitere Variablen zurückzuführen,
die nicht berücksichtigt wurden (ihm wird in der multivariaten
Statistik große Aufmerksamkeit gewidmet).
.
Dieser Fehler ist in der Regel auf weitere Variablen zurückzuführen,
die nicht berücksichtigt wurden (ihm wird in der multivariaten
Statistik große Aufmerksamkeit gewidmet).
Es läßt sich nun zeigen, daß der Determinationskoeffizient in seiner Definition als
![]()
identisch ist mit dem Quadrat des Korrelationskoeffizienten r (Herleitung vgl. Litz 1997: 162 ff.). Dies bedeutet, daß man lediglich den Korrelationskoeffizienten r quadrieren muß, um die Aussage treffen zu können: "x Prozent der Varianz von Y sind durch die Varianz der Variable X erklärbar."
Damit sind r und r2 auch für Zwischenwerte sehr gut empirisch interpretierbar.
![]() Übungen
Übungen
Berechnen Sie für die bisher behandelten Beispiele noch einmal (maschinell) den Korrelationskoeffizienten und interpretieren Sie die Ergebnisse.
Je nach Bedarf rechnen Sie
die folgende Aufgabe einmal von Hand durch:
Aufgabe
als pdf laden / Lösung
als pdf laden
Erforschen Sie mit der folgenden
Simulation, wie stark sich einzelne Extremwerte (Ausreißer)
auf den Korrelationskoeffizienten auswirken. Sie können dabei
einen Punkt beliebig verändern, während die übrigen
Merkmalsausprägungen unverändert bleiben:![]() Präsentation
laden!
Präsentation
laden!