Regression und Korrelation

Lineare Regression

Wir kennen nun bereits Methoden um für Variablen auf nominalem und ordinalem Skalenniveau die Stärke des statistischen Zusammenhanges zu bestimmen. Dabei waren jeweils die sich aus dem Skalenniveau ergebenden Beschränkungen zu berücksichtigen, wie etwa, daß auf ordinalem und nominalem Skalenniveau keine Differenzen berechnet werden können (mit einigen Ausnahmen im Falle der Rangkorrelation für ordinalskalierte Daten).

Metrische Daten lassen sich hingegen gut durch mathematische Funktionen darstellen, d.h. wir betrachten die abhängige Variable als Funktion der unabhängigen Variablen und suchen nach einer Funktion, mit der sich die Art und Richtung des Zusammenhanges möglichst gut darstellen läßt.

Wir betrachten in diesem Semester die einfache lineare Regression. Dies bedeutet zum einen, wir gehen davon aus, daß es nur eine abhängige und eine unabhängige Variable gibt und wir unterstellen einen linearen Zusammenhang zwischen den Variablen - nehmen also an, daß sich die abhängige Variable mehr oder weniger gut als lineare Funktion (Geradengleichung) der unabhängigen Variablen darstellen läßt.

Um die gesuchte Funktion zu erhalten, muß also ein Weg gefunden werden, die beiden Parameter der Geradengleichung Steigung b und Achsenabschnitt a zu bestimmen.

Beachten Sie: eine negative Steigung bedeutet einen negativen Zusammenhang, eine positive Steigung einen positiven Zusammenhang!

Die Logik des Modell ist relativ einfach:

Stellt man die Ausprägungen der beiden Variablen X und Y in einem Koordinatensystem dar, wobei für jeden Merkmalsträger jeweils ein Punkt an den Koordinaten (X;Y) eingezeichnet wird, so erhält man eine sogenannte Punktwolke, die meist schon einen ersten Eindruck davon vermittelt, ob und in welcher Richtung ein Zusammenhang vorliegt. Im Falle eines vollständigen Zusammenhanges würden alle Punkte auf einer (unsichtbaren) Geraden liegen, im Falle der Unabhängigkeit würden die Punkte kugelförmig streuen.

Man versucht nun, durch diese Punktwolke eine Gerade zu liegen, für die die Summe der quadrierten Abstände (quadrieren, weil die Summe der einfachen Abstände Null ergibt) den geringsten Wert aller denkbaren Geraden annimmt.

Übung:

Spielen Sie ein wenig mit dieser Präsentation. Sie ermoglicht Ihnen, per Mausklick in das Koordinatensystem eine beliebige Punktwolke anzuordnen. Dabei wird automatisch die Regressionsgerade, und auf Wunsch auch die Abstände der einzelnen Punkte von der Regressionsgerade (die sog. Residuen) eingezeichnet.

Haben Sie bitte etwas Geduld, falls der Ladevorgang etwas länger dauern sollte. Da diese Anwendung direkt aus den USA geladen wird, kann es ja nach Tageszeit etwas dauern.

Nun ist die Frage: Wie bestimmt man Steigung und Achsenabschnitt, um die Regressionsgerade so ermitteln zu können, wie sie es in obigem Beispiel gesehen haben?

Zunächst wird die Steigung bestimmt. Die Formel dafür lautet:

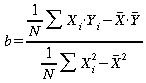für Einzelwerte bzw.

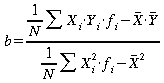für gruppierte Daten

Herleitung vgl. Litz 1997: 156

Anschließend ergibt sich a durch Einsetzen in:

und wir erhalten die Regessionsgerade

Dies ist also diejenige Geradengleichung, die sich mit den geringsten Abstandsquadraten durch die Punktwolke legen läßt. Mit Hilfe der Regressionsgeraden sind durch einfaches Einsetzen auch Prognosen für nicht empirisch vorgefundene Merkmalsausprägungen möglich (z.B. Wie hoch wäre die Konsum Y bei einem Preis von X?).

Dabei ist klar, daß die Regressionsgerade noch nichts über die Stärke des Zusammenhanges aussagt. Je geringer der Zusammenhang, desto ungenauer werden auch die Prognosen sein. Mit dieser Frage werden wir uns im Zusammenhang mit der Korrelation beschäftigen.

Lösen Sie bitte folgende Aufgabe:

Gelegentlich behaupten Politiker: Wenn "die Wirtschaft" erst einmal wächst, dann nimmt auch die Arbeitslosigkeit ab. In Tabelle A sind einige wirtschaftsstatistische Daten verzeichnet. Sind Ihrer Meinung nach diese Daten geeignet, die o.g. Behauptung zu überprüfen?

Tabelle A:

Quelle: StBA: Wirtschaft und Statistik, 1960, S.11 und 30, eigene Berechnungen

Tabelle B:

Quelle: StBa: Wirtschaft und Statistik, 1987/1, S.6f

1. Formulieren Sie auf der Grundlage der in Tabelle A aufgeführten Daten eine Hypothese in Form einer Gleichung!

2. Stellen Sie den Zusammenhang graphisch dar!

3. Berechnen Sie die Regressionsfunktion und zeichnen Sie ihren Graphen. Versuchen Sie zu beurteilen, ob die unter 1) formulierte Hypothese "gut" ist.

4. Fertigen Sie aus den Daten aus Tabelle B eine Graphik an und berechnen Sie die Regressionsfunktion!

5. Welche Arbeitslosigkeit wäre bei einem BSP von 1579 Mrd. DM zu erwarten?

6. Vergleichen Sie die Ergebnisse aus 3) und 4) und versuchen Sie eine Interpretation der Unterschiede. Wäre es eventuell sinnvoll, eine Regressionsfunktion für den gesamten Zeitraum 1952 bis 1987 zu berechnen?

Lösen Sie die Aufgabe zunächst unbedingt von Hand, da Sie diese Fähigkeit für die Klausur benötigen!! Fertigen Sie dazu eine Arbeitstabelle mit folgenden Spalten an: