Statistische Unabhängigkeit

Sind zwei Variablen X und Y statistisch völlig unabhängig, so weist die zweidimensionale Häufigkeitsverteilung folgende Eigenschaften auf:

1. Die bedingten relativen Häufigkeiten f`(X_j|Y_i) sind für alle i,j gleich.
   Dies ist offensichtlich, da bei Unabhängigkeit der Variablen die Ausprägungen der unabhängigen Variablen eben keinen Einfluß auf die Ausprägungen der „abhängigen“ Variablen haben.

2. Die bedingten relativen Häufigkeiten f`(X_j|Y_i) sind gleich den einfachen relativen Häufigkeiten
   Auch dies ist an sich trivial, da bei statistischer Unabhängigkeit die Bedingung durch die Merkmalsausprägungen der unabhängigen Variablen keine Auswirkung auf das Auftreten der Merkmalsausprägungen der "abhängigen" Variablen haben.

3. Die relative Häufigkeit des gemeinsamen Auftretens zweier Variablen entspricht dem Produkt der bedingten relativen Häufigkeit des Merkmals der einen und der einfachen relativen Häufigkeit des Merkmals der anderen Variablen

4. Die relative Häufigkeit des gemeinsamen Auftretens entspricht dem Produkt der einfachen relativen Häufigkeiten der beiden Variablen.

Völlige statistische Unabhängigkeit im Sinne dieser vier Sätze wird in der empirischen Praxis natürlich so gut wie nie zu finden sein. Sie stellen also noch keine ausreichende Möglichkeit dar, Aussagen über statistische Zusammenhänge zwischen zwei Variablen zu machen. Das eigentlich Wichtige ist aber, daß in Anwendung der Sätze zur stat. Unabhängigkeit jene absoluten Häufigkeiten errechnet werden können, die bei statistischer Unabhängigkeit zu erwarten wären. Der nächste logische Schritt ist dann, zu betrachten wie stark die empirischen Häufigkeiten von den erwarteten Häufikeiten abweichen und auf dieser Basis Maßzahlen für die Stärke des Zusammenhangs zu konstruieren.

Aus Satz 4 ergibt sich duch Multiplikation mit N:

bzw.

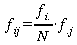
Somit lassen sich aus den Randbedingungen (den Zeilen- und Spaltensummen) die absoluten Häufigkeiten bestimmen, die im Falle der Unabhängigkeit der beiden Variablen zu erwarten wären.

Die Tabelle, die diese Werte enthält, nennt man Indifferenztabelle - während die Tabelle der empirisch vorgefundenen zweidimensionalen Häufigkeitsverteilung als Kontingenztabelle bezeichnet wird.

Betrachten Sie zunächst ein Beispiel zur Berechnung der Indifferenztabelle: