 |
Beispiele und Aufgaben im Modul Normalverteilung
3. Beispiele und Aufgaben zum Vergleich einer empirischen mit einer Normalverteilung
a) Beispiele
Eine Befragung von einigen Hundert Studenten über die Höhe der Mietausgaben hat ergeben, dass 8,5% weniger als 130 EUR und 14,5% zwischen 130 und unter 150 EUR Miete zahlen.
Die gesamten empirischen Daten weisen eine Durchschnittsmiete von 175 EUR und eine Standardabweichung von 35 EUR auf.
Im Folgenden soll geprüft werden, ob die empirischen Daten denen aus einer Normalverteilung entsprechen und die Prozente der empirischen Verteilung mit den Wahrscheinlichkeitem für diese beiden Segmente unter einer Normalverteilung vergleichbar sind.
-
Beispielsaufgabe 1: Skizzieren Sie beide
Verteilungen bzgl. ihrer Parameter!
Antwort: Die Normalverteilung weist die gleichen Parameter auf wie die empirische Verteilung, also: μ = 150 EUR und σ = 35 EUR.
-
Beispielsaufgabe 2: Wie groß wäre demnach die Wahrscheinlichkeit, zufällig
eine(n) Studierende(n) anzutreffen mit einer Miete unter 130 EUR? Formulieren Sie genau
die Bestimmung der Wahrscheinlichkeiten der Besetzung dieser Klasse.
Antwort:
P(x < 130) = 1 - F(x = 130) = 1 - F(z). Die Z-Transformation ergibt: z = (130 - 175)/35 = - 1,29. -
Die Wahrscheinlichkeit 1 - F(z = -1,29) entspricht der Wahrscheinlichkeit F(z = 1,29) = 0,0985. Die Wahrscheinlichkeit beträgt demnach 9,85%.
-
Beispielsaufgabe 3: Wie groß wäre dann die Wahrscheinlichkeit, zufällig
eine(n) Studierende(n) anzutreffen mit einer Miete von 130 bis unter 150 EUR?
Antwort: Die bearbeitung dieser Aufgabe besteht in zwei Schritten:
-
der Bestimmung der Wahrscheinlichkeit P(x < 150) = 1 - F(x = 150).
Diese Teillösung ergibt in Analogie zum vorherigen Lösungsweg: P(x < 150) = F(x < -0,71) = 0,2388
und der Ermittlung der Differenz F(x = 150) - F(x = 130) = 0,2388 - 0,0985 = 0,1403.
Die Wahrscheinlichkeit beträgt demnach 14,03%.
Beispielsaufgabe 4: Welche Miete zahlen unter obiger
Verteilungsannahme die 5% am teuersten wohnenden Studierenden?
Antwort: Gesucht ist z in F(z): F(z) = 0,05, z = 1,65.
Dazu wird die Z-Transformation nach x aufgelöst: z = 1,65 = (x - 175)/35, d.h. x = 175 + 1,65 · 35 = 232,75 EUR -
Die 5% teuersten Wohnungen kosten mindestens 232,75 EUR Miete pro Monat.
Anmerkung: Eine graphische Darstellung der Lösung und der Lösungsweg finden sich in den Musterlösungen zur Aufgabe 21 (vgl. Link am Ende des Kapitels).
b) Aufgaben
-
Aufgabe 1:
Im Folgenden soll geprüft werden, ob die kompletten empirischen Daten der Tabelle II-4 denen aus einer Normalverteilung entsprechen und die Prozente der empirischen Verteilung für die weiteren Klassen mit den Wahrscheinlichkeitem einer Normalverteilung übereinstimmen.
Berechnen Sie die Werte der theoretischen Verteilung und geben Sie diese bitte in der Form x,xx ein, also in Prozent und auf zwei Nachkommastellen gerundet!
Tabelle II-4: Reale Mietausgaben im Vergleich zur Normalverteilung
-
Aufgabe 2:
Welche Miete zahlen unter obiger
Verteilungsannahme die 1% am teuersten wohnenden Studierenden?
3. Beispiele und Aufgaben zur Approximation einer Binomialverteilung durch eine Normalverteilung
a) Beispiel zur Approximation einer Binomialverteilung durch eine Normalverteilung
Im Jahre 2015 gaben etwa 70% der 18 - 29 Jährigen an, im Urlaub gerne neue Länder kennenlernen zu wollen. Wie groß ist die Wahrscheinlichkeit in einer Stichprobe von n = 100 zwischen 60 und 80 junge Erwachsene mit diesem Urlaubswunsch zu finden?
Gefragt ist damit nach der Wahrscheinlichkeit einer diskreten Variablen k: P (60 ≤ k ≤ 80) ?
Wir prüfen zuerst, ob die diskrete Binomial-Verteilung der Variablen hinreichend durch eine Normalverteilung approximiert werden kann. Die Approximationsbedingung lautet:
n · p(1-p) ≥ 9, konkret: 100 · 0.7(1-0.7)= 21 ≥ 9. Damit ist die Bedingung erfüllt.
Nun definieren wir die gesuchte Wahrscheinlichkeit für eine Normalverteilung. Unter Berücksichtigung der Stetigkeitskorrektur ergibt sich diese Wahrscheinlichkeit als:
P(60 - 0.5 ≤ x ≤ 80 + 0.5).
Wir bestimmen danach die Parameter der Normalverteilung: x hat einen Erwartungswert von 70:
E(X) = n · p = 100 · 0.7 = 70
und eine Varianz von 21:
VAR(X) = n · p(1-p) = 100 · 0.7(1- 0.7) = 21.
-
Als Wahrscheinlichkeit für die standard-normalverteilte Variable z ergibt sich demnach:
-
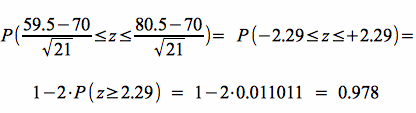
Damit beträgt die Wahrscheinlichkeit, dass in einer Stichprobe von 100 18 - 29 Jährigen mit diesem Urlaubswunsch angetroffen werden, fast 98%.
Mit diesem externen
Applet der Rice University können Sie die Approximationsgüte graphisch und rechnerisch
für unterschiedliche Bedingungen veranschaulichen.
b) Aufgabe
Eine Partei hat bei der nächsten Wahl 5% aller Stimmen zu erwarten.
Aufgabe 1: Wie gross ist die Wahrscheinlichkeit, dass bei einer Befragung von 1000 Personen genau 50 angeben, diese Partei zu wählen?
 Diese Aufgabe können Sie in 5 Schritten mit diesem interaktiven Tool bearbeiten. Vor dem ersten Einsatz dieses Übungstools oder bei Problemen empfiehlt es sich, die Hinweise in
dieser pdf-Datei zu berücksichtigen.
Aufgabe 2: Wie gross ist die Wahrscheinlichkeit, dass bei einer Befragung von 1000 Personen 50 Personen oder weniger angeben diese Partei zu wählen?
Diese Aufgabe können Sie in 3 Schritten mit diesem interaktiven Tool bearbeiten.
Zur
Musterlösung der Aufgaben
(19) bis (21).
|
