|
Die mehrfaktorielle Varianz- und Kovarianzanalyse mit SPSS - Beispiele und Aufgaben im Modul XII-7 Die mehrfaktorielle Varianz- und Kovarianzanalyse
1. Die univariaten linearen Analyse-Modelle
Die varianz-/kovarianzanalytischen Rechenprogramme von SPSS basieren auf der Umrechnung der Faktoren und ihrer Wechselwirkungen in Dummy-Variablen. Die Varianzanalysen werden deshalb wie Regressions- und Korrelationsanalysen durchgeführt.
Mit dem Modul "Analysieren > Allgemeines lineares Modell > Univariat.." bietet SPSS ein komplexes Tool zur mehrfaktoriellen Varianzanalyse und zur Kovarianzanalyse an.
Über die Modellspezifikation lassen sich die verschiedenen Ansätze des Einbezugs der Faktoren und Kovariaten steuern. Präsentiert werden hier:
das gesättigte Modell, in dem alle Faktoren und alle Wechselwirkungen berücksichtigt werden. Dieses Modell entspricht in seiner Konzeption dem Einschluss-Modell der multiplen Regressionsanalyse. Dabei werden alle Komponenten, d.h. die Faktoren und die Wechselwirkungen in einem Zug in die Analyse einbezogen.
das angepasste Modell, in dem nur noch die tatsächlich relevanten Faktoren und Wechselwirkungen enthalten sind und
das hierarchische Modell, bei dem die Faktoren und die Wechselwirkungen nach einer kausalen Anordnung entsprechend der Reihung im Eingabefeld berücksichtigt werden.
das kovarianzanalytische Modell, in dem zu den nicht-metrischen Faktoren metrisch-skalierte "Kovariate" hinzutreten.
Die Beispielsrechnungen werden wieder mit den Daten der Datei Partizipation_1.sav und der dort enthaltenen, metrisch-skalierten Variablen "Partizipationsprofil" sowie der jetzt explizit als nicht-metrisch behandelten Kontrollvariablen "Status", "Ausbildung" und "Geschlecht" durchgeführt. Im Rahmen einer Kovarianzanalyse tritt dann noch die Kovariate "gewünschte Beteiligung - Partpot" hinzu.
Dabei soll u.a. im Vergleich zur multiplen Regressionsanalyse (vgl. Modul 12-6) auf der Basis dort unterstellter metrischer Skalierung der Variable Status und Ausbildung geprüft werden, ob und wie weit der Zusammenhang zwischen der tatsächlichen Beteiligung und den Faktoren durch die (korrekte) Behandlung dieser Kontrollvariablen als ordinale Faktoren beeinflusst wird und welche Veränderungen sich im Hinblick auf die Stärke des Zusammenhangs ergeben.
a) Das mehrfaktorielle gesättigte Modell
In der Beispielsrechnung wird die Abhängigkeit der Variablen "Partizipationsprofil" von den Faktoren "Status", "Ausbildung" und "Geschlecht" sowie den zwei- und dreifachen Wechselwirkungen untersucht.
Der Aufruf des Tools
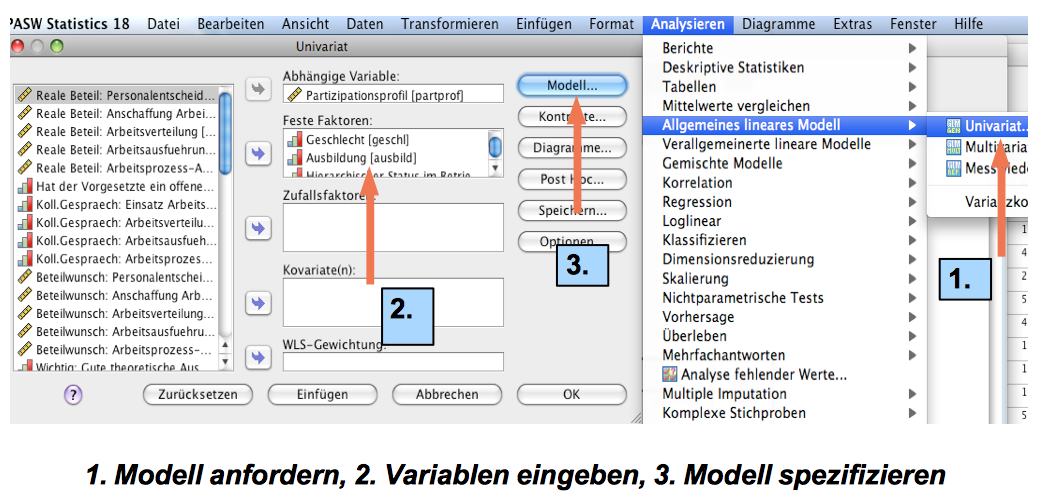
Screenshot 12-47: Die Anforderung der mehrfaktoriellen Varianzanalyse (gesättigtes Modell)
Anmerkungen:
Die Faktoren werden (wie im Beispiel) ins Fenster "Feste Faktoren" eingegeben, wenn die Faktorstufen (d.h. die Kategorien) der Faktoren vorab festgelegt wurden und für alle Stufen auch Beobachtungen vorliegen. Man spricht dann von einer Varianzanalyse mit festen Effekten .
Wenn die Faktorstufen (d.h. die Kategorien) der Faktoren als offene Kategorien erhoben wurden oder nicht für alle Stufen Beobachtungen vorliegen, werden die Faktoren ins Fenster "Zufallsfaktoren" eingegeben. In diesem Fall liegt eine Varianzanalyse mit zufälligen Effekten vor.
Die Modellspezifikation des gesättigten Modells"
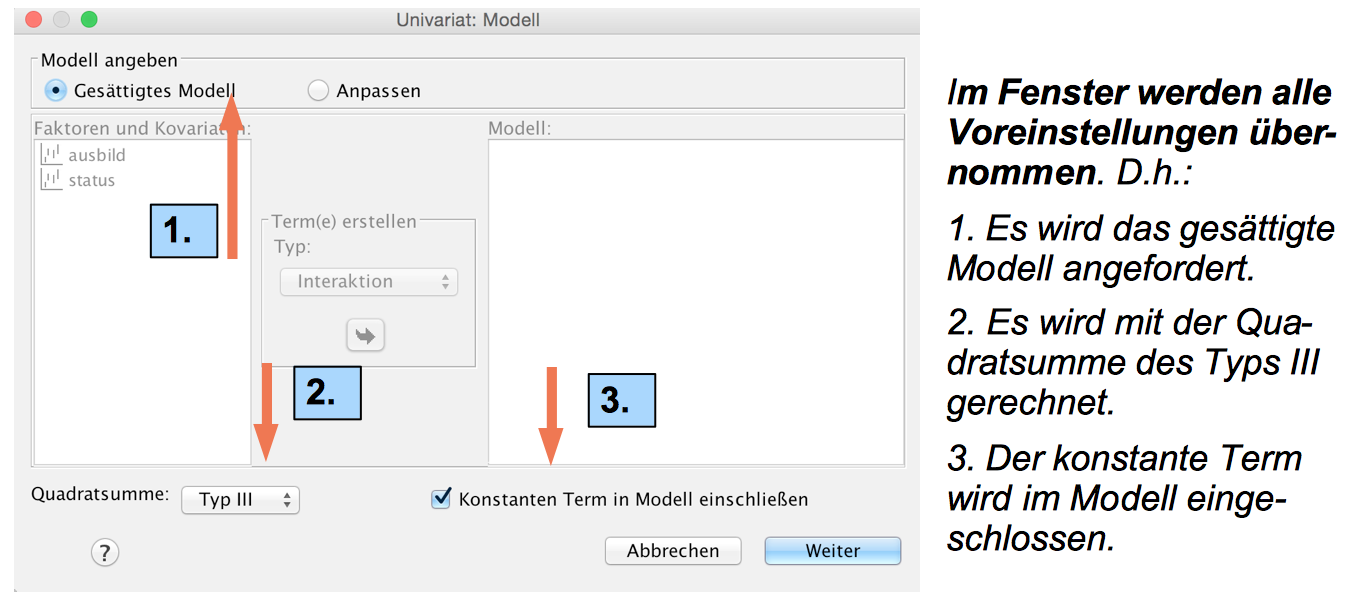
Screenshot 12-48: Die Modellspezifikation
Anmerkungen:
-
zu 1: Im gesättigten Modell wird der gemeinsame Beitrag aller drei Faktoren und ihrer Wechselwirkungen nachgewiesen.
-
zu 2 Festlegung der Quadratsummen:
Mit der Wahl des Typs der Quadratsummen werden die Erklärungsbeiträge der Modellkomponenten gesteuert. Vorgestellt werden der beiden gebräuchlichsten und aus der multiplen Regressionsanalyse bereits bekannten Typen.
-
Mit dem Typ III (Voreinstellung) werden aus den Beiträgen der einzelnen Komponenten die Wirkungen der anderen Faktoren und der Wechselwirkungen auspartialisiert. Er entspricht in der multiplen Regressionsanalyse der Methode "Einschluss".
-
Typ I generiert ein hierarchisches Modell wie es unter Punkt c) vorgestellt wird.
-
zu 3: Wird die Konstante aus dem Modell ausgeschlossen, wird unterstellt, dass die Regressionsfunktion durch den Ursprung geht. Da dies i.A. nicht der Fall ist, sollte diese Voreinstellung nicht verändert werden, um nicht unsinnige Ergebnisse zu erhalten.
Die Ergebnisse
Screenshot 12-49: Die ANOVA-Tabelle

Die Interpretation der Ergebnisse
Im gesättigten Modell erklären die drei Faktoren Status, Ausbildung und Geschlecht sowie ihre zweifachen und dreifachen Wechselwirkungen 58,2% der Varianz der abhängigen Variablen Partizipationsprofil. Der Determinationskoeffizient der Varianzanalyse liegt damit um etwa 15% über der der Regressionsanalyse, in der die Faktoren noch als metrische Variablen behandelt wurden (vgl. dazu die
Beispielsrechnungen zur multiplen Regressionsanalyse , Screenshot 12-44).
Ausgangsbasis der Berechnung von R-Quadrat ist die SAQ-Gesamt, die im Output als "Korrigierte Gesamtvariation" bezeichnet wird. Diese wird aufgespalten in eine SAQ des "Korrigierten Modells" (im vorherigen Modul als SAQ-zwischen bezeichnet), die den Einfluss aller Komponenten ausdrückt, und in die Fehler-SAQ, d.h. die nicht erklärte SAQ.
Die Modellkomponenten sind nicht alle signifikant, vor allem der Faktor "Ausbildung" sowie alle Wechselwirkungen. Dies liegt daran, dass entgegen der Logik auch Einflüsse von hierarchisch nachrangigen Komponenten auspartialisiert wurden
(vgl. dazu die Diskussion im Modul Konzepte und Definitionen zur multiplen Regressionsanalyse , Punkt 5 c, insbes. die Abb. 12-24 und 12-25).
Nicht signifikanten Komponenten lassen sich im angepassten Modell ausschalten bzw. in einer hierarchischen Analyse korrekt einbinden.
Anmerkung:
.
Das Testverfahren für die Komponenten findet sich in
ViLeS 2, Modul "Test der Regressions- und Korrelationskoeffizienten, Teil C Die Tests der η2-Koeffizienten in der ein- und mehrfaktoriellen Varianzanalyse"
b) Das mehrfaktorielle angepasste Modell
Die Anpassung des Modells
Im angepassten Modell sollen alle Komponenten des gesättigten Modells (vgl. Screenshot 12-49) ausgeschlossen werden, deren Signifikanz größer als ,100 ist.
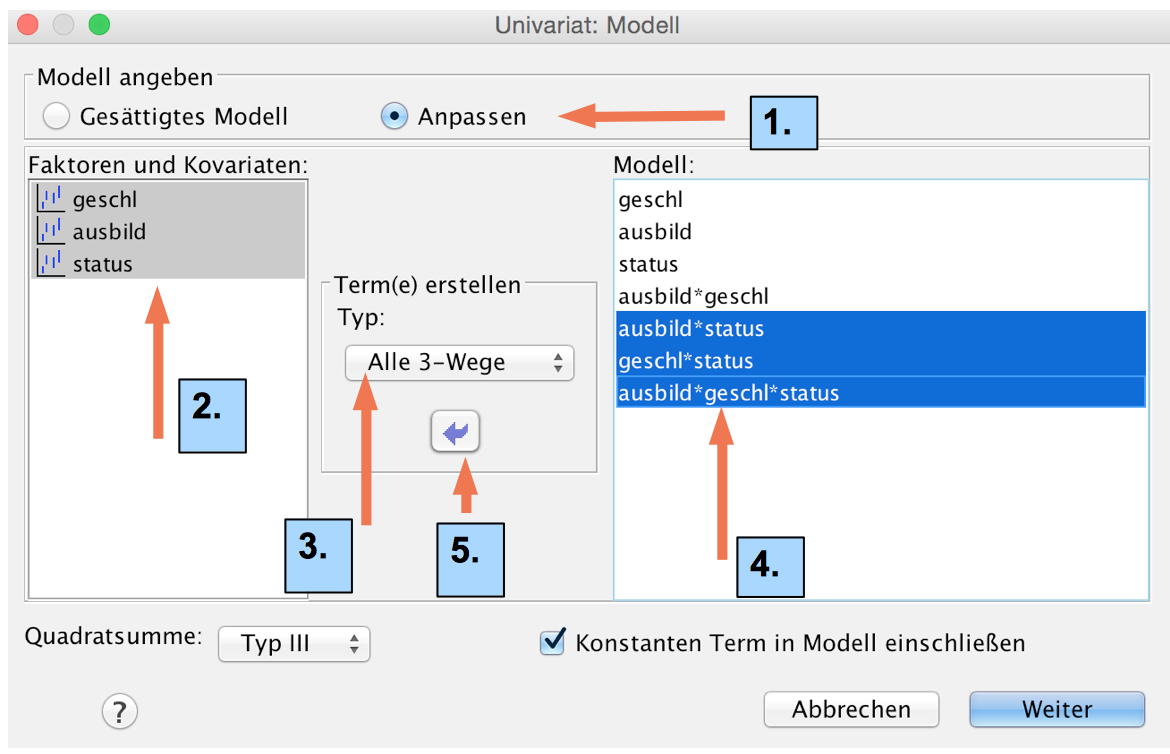
Die Anpassung erfolgt über eine Modifikation der Modellspezifikation. Die nicht-signifikante Wechselwirkungen werden aus dem Modell in der Hoffnung eliminiert, dass damit die Faktoren Ausbildung und Geschlecht sowie die Wechselwirkung "ausbild*geschl" einen ausreichend Erklärungsbeitrag liefern.
|
Screenshot 12-50: Die Spezifikation des angepassten Modells
|
|

|
|
|
Die Modellergebnisse
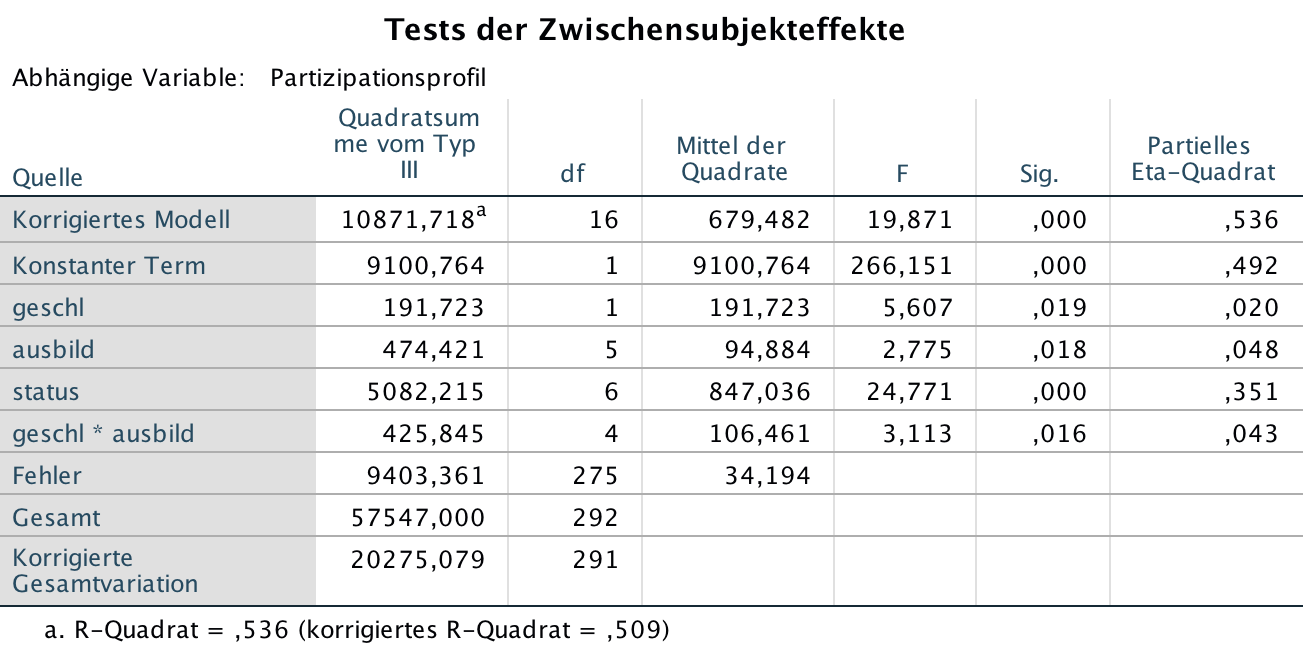
Screenshot 12-51: Die ANOVA-Tabelle und die Effekte des angepassten Modells
Die Interpretation der Ergebnisse
Im angepassten Modell wird der gemeinsame Beitrag der drei Faktoren Status, Ausbildung und Geschlecht sowie die Wechselwirkung "gesch*ausbild" nachgewiesen. Ihr gemeinsamer Erklärungsbeitrag liegt mit knapp 54% etwas unter dem des gesättigten Modells mit 58%.
Mit der Elimination der nicht gewünschten Wechselwirkungen aus dem Modell erreichen die Faktoren Geschlecht und Bildung sowie die Wechselwirkung "gesch*ausbild" eine gerade noch akzeptable Signifikanz von etwas unter 2%.
-
Da aus den Beiträgen der einzelnen Komponenten die Wirkungen der jeweils anderen Faktoren und Wechselwirkungen auspartialisiert wurde, addieren sich die partiellen Beiträge nicht zum Gesamtbeitrag.
-
Wenn man die den Komponenten zuordenbaren partiellen Quadratsummen zusammenfasst, ergibt sich ein Betrag von 6174,213 (vgl. Screenshot 12-51), d.h. von der SAQ des korrigierten Modells (= 10871,718) steht eine SAQ von 4697,514 (d.h. 43,2 %) aufgrund der Abhängigkeiten innerhalb der Faktoren nicht für eine Prüfung der Signifikanz und eine Erklärung des Beitrags der einzelnen Komponenten zur Verfügung.
-
Welche Konsequenzen das für das Konzept der Effekte hat und wie dieser Mangel zu beheben ist, zeigen die nächsten Abschnitte.
-
Die Erklärung und Interpretation der Effekte (d.h. der partiellen eta-Quadrate in der letzten Tabellenspalte) erfolgt in Abschnitt 2.a).
c) Das mehrfaktorielle hierarchische Modell
Die Modellstruktur
Das mehrfaktorielle hierarchische Modell modifiziert den Gesamterklärungsbeitrag des angepassten Modells so, dass die Quadratsumme des korrigierten Modells vollständig auf die Modellkomponenten aufgeteilt wird.
Das hierarchische Modell basiert auf der kausalen Struktur im Variablensatz, wie sie im
im Modul Konzepte und Definitionen zur multiplen Regressionsanalyse , Punkt 5 b, in Abb. 12-22 skizziert wurde.
Die Reihenfolge, in der die Komponenten in das Kalkül einbezogen werden, entspricht der Abfolge der in den Screenshots 12-47 und 12-50 gelisteten Terme:
Als erster Faktor wird die unabhängigste Variable, der Faktor "Geschlecht" eingegeben.
Daraufhin folgen nacheinander die Faktoren "Ausbildung" und "Status".
Den Abschluss bildet die Wechselwirkung "geschl*ausbild".
Der Aufruf des hierarchischen Modells und die Anforderung der partiellen eta-Quadrate
Die zur Steuerung des Prozesses notwendige Modifikation des angepassten Modells besteht im Wechsel der Quadratsumme von "Typ III" zu "Typ I" in der Modellspezifikation (vgl. Screenshot 12-48, Punkt 2).
Die Varianzzerlegung im hierarchischen Modell
Screenshot 12-52: Die ANOVA-Tabelle des hierarchischen Modells
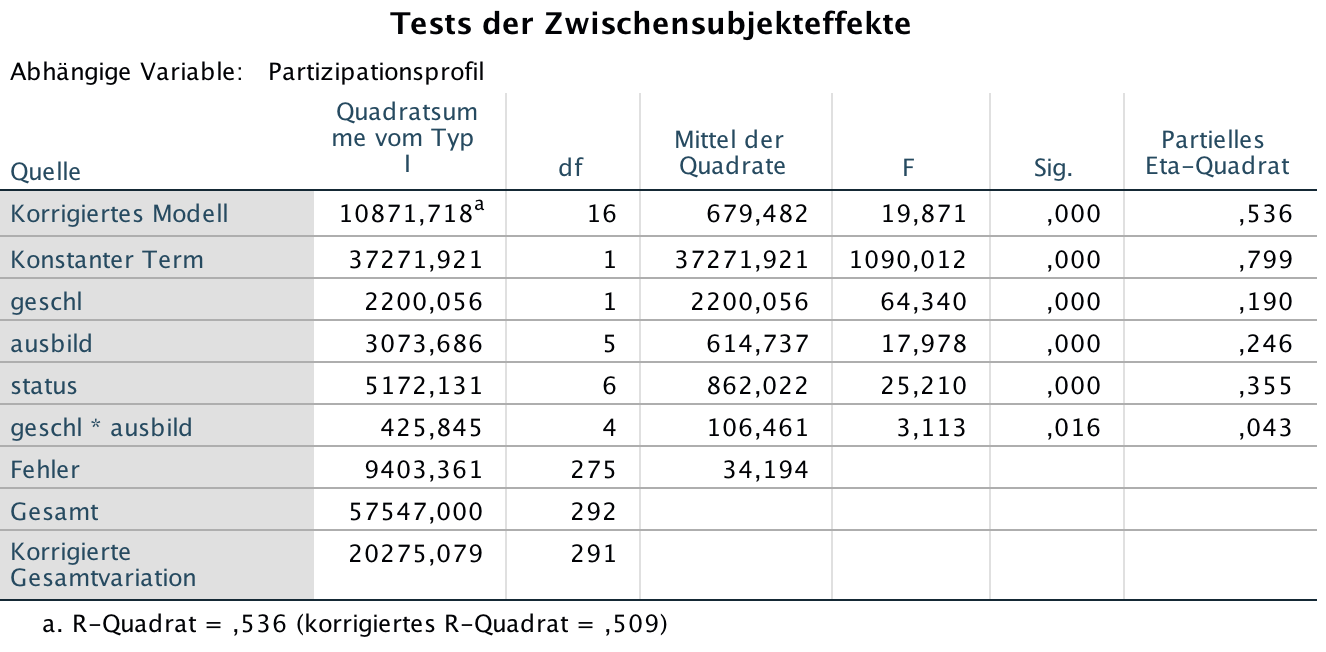
Die Interpretation der Quadratsummen
Im Vergleich zum angepassten Modell mit nach Typ III gebildeten Quadratsummen (vgl. Screenshot 12-51) zeigt sich:
- Die insgesamt erklärten Quadratsummen sind identisch, aber anders auf die Faktoren aufgeteilt.
- Der dem Faktor Geschlecht zukommende Erklärungsbeitrag steigt von 191 auf 2200, was mehr als einer Verzehnfachung entspricht.
- Der Zuwachs des Faktors Ausbildung (als Partialvariable "ausbild - geschl") führt zu einer mehr als Versechsfachung der Quadratsumme (von 474 auf 3073) und ist damit hochsignifikant.
- Der Faktor Status (als Partialvariable "status- geschl,ausbild") kann, trotz der Zuwächse der prioritären Faktoren, seinen Erklärungsbeitrag leicht verbessern (5172 gegenüber 5082).
- Für die zuletzt einbezogen Komponente, die Wechselwirkung, bleibt der Beitrag ansatzgemäß konstant.
- Damit sind die vorher "unterbewerteten" Faktoren "Geschlecht" und "Ausbildung" nun ebenfalls mit einem Niveau von 0,000 hoch signifikant.
d) Das kovarianzanalytische Modell
Die Modellstruktur
In der Beispielsrechnung wird die Abhängigkeit der Variablen "Partizipationsprofil" von den Faktoren "Status", "Ausbildung" und "Geschlecht", den zweifachen Wechselwirkungen und dem Kofaktor "Partizipationspotential" untersucht.
Dabei wird zu Vergleich mit dem multiplen Regressionsmodell in Abschnitt "Beispiele und Aufgaben" des Moduls XII-6 ein hierarchischer Ansatz gewählt, der den Gesamterklärungsbeitrag wieder vollständig auf die Modellkomponenten aufgeteilt.
Die Vorgehensweise basiert auf der kausalen Struktur im Variablensatz, wie sie im Modul XII-6 in Abb. 12-22 skizziert wurde (siehe obigen link).
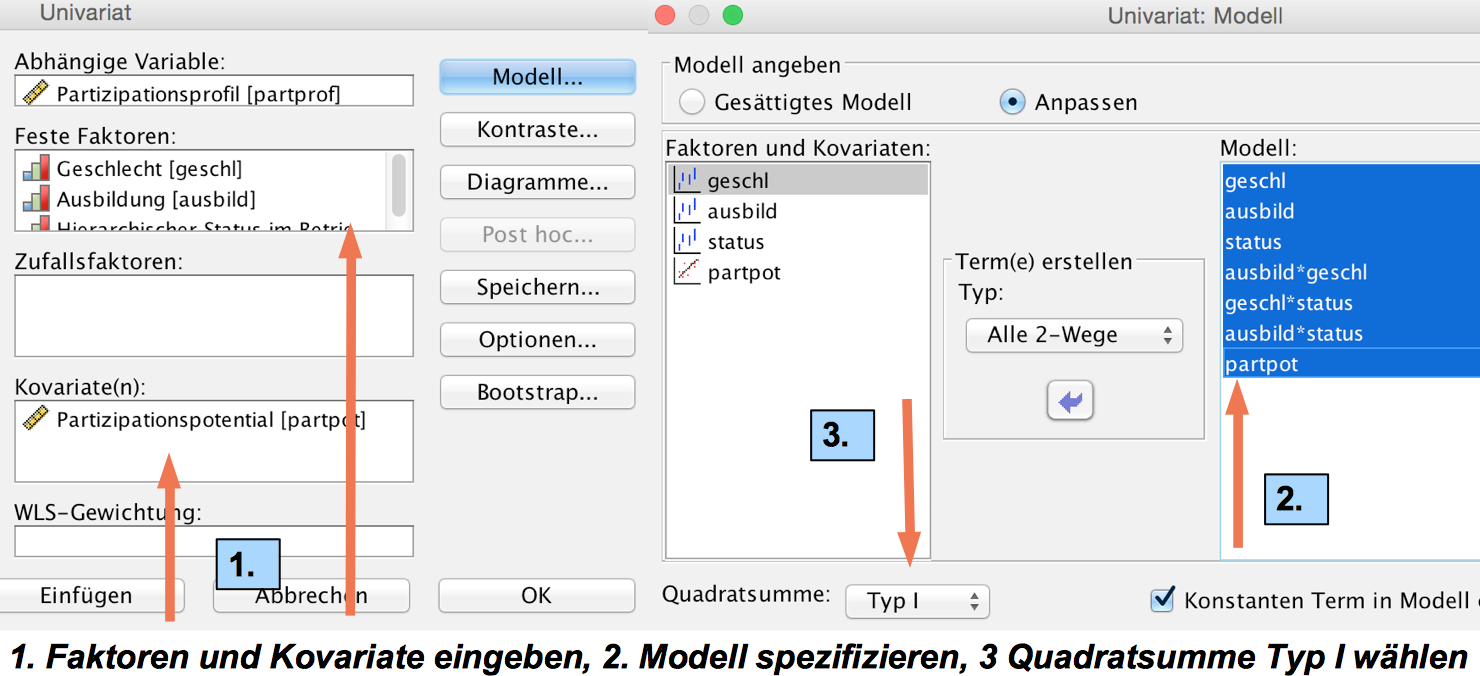
Die Reihenfolge, in der die Komponenten in das Kalkül einbezogen werden, entspricht der Abfolge der im Screenshot 12-53 unter Punkt 2 gelisteten Terme:
Als erstes werden die Faktoren "Geschlecht", "Ausbildung" und "Status" eingegeben.
Daraufhin folgen die zweifachen Wechselwirkung der Faktoren.
Den Abschluss bildet die Kovariate "Partizipationspotential".
Das hierarchische Modell wird mit der Wahl der Quadratsumme des "Typ I" in der Modellspezifikation erzeugt.
Der Aufruf des Modells
Screenshot 12-53: Die Anforderung des Kovarianz-Modells
Die Varianzzerlegung im hierarchischen kovarianzanalytischen Modell
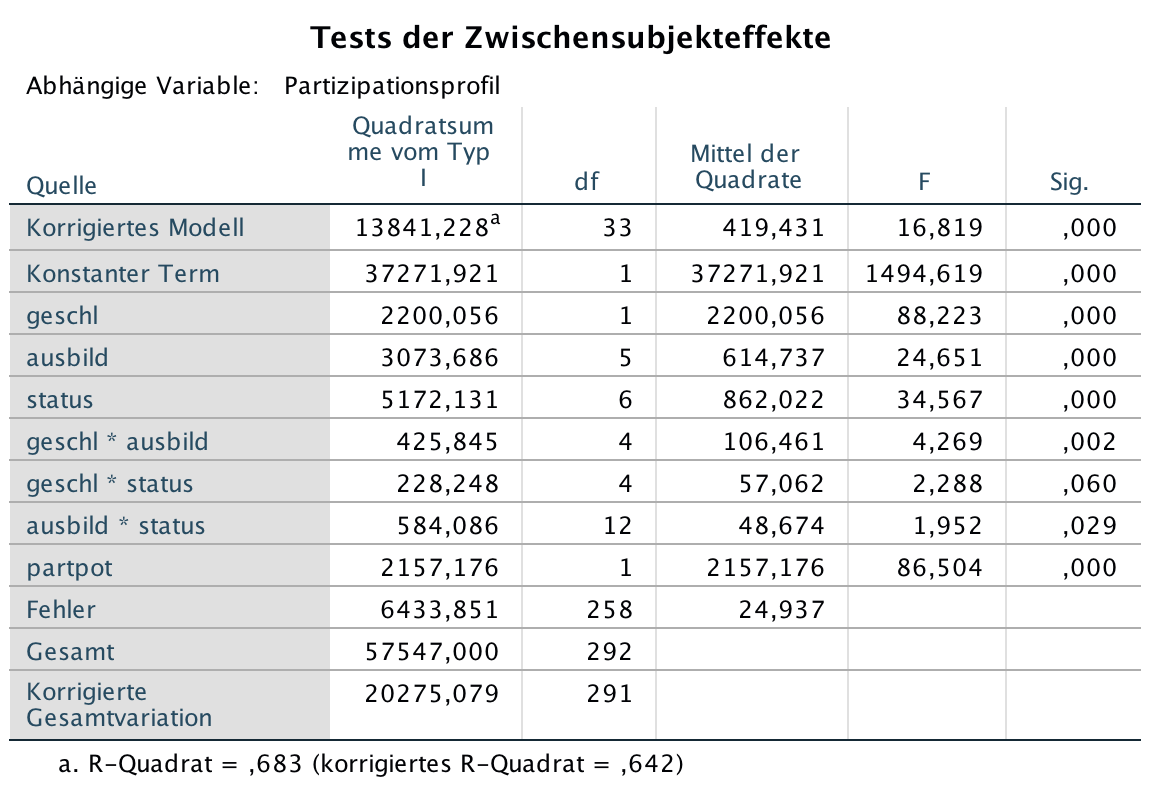
Screenshot 12-54: Die ANOVA-Tabelle des Modells
Die Interpretation der Modellergebnisse
Die im Modell enthaltenen Komponenten erklären insgesamt etwa 68% der Varianz der Variablen Partizipationsprofil.
Dieses Ergebnis ist einmal zu beziehen auf das gesättigte varianzanalytische Modell (vgl. Screenshot 12-49). Dieses enthält zusätzlich noch die (nicht-signifikanten) 3-fachen Wechselwirkungen aber nicht die Kovariate und erklärt dabei nur etwa 58% der Gesamtvarianz.
Zum anderen kann das Ergebnis verglichen werden mit dem aus der multiplen Regressions- und Korrelationsanalyse, bei der die Faktoren nicht ganz korrekt als metrische Variablen behandelt wurden. Dort werden knapp 60% der Gesamtvarianz erklärt (vgl. Screenshot 12-44).
Da die zweifachen Wechselwirkungen "geschl*status" und "status*ausbild" sowie die Kovariate logischerweise nach den Faktoren und der Wechselwirkung "geschl*ausbild" eingegeben werden, sind aus ihnen die Einflüsse der bereits einbezogenen Komponenten auspartialisiert.
Ihr Erklärungsbeitrag (in der Regressionsanalyse als Änderungen in R-Quadrat tabellarisch ausgewiesen) muss hier per Hand berechnet werden. Er beträgt für die Wechselwirkungen "geschl*status" 1,13% und "status*ausbild" 2,88% sowie für die Kovariate immerhin 10,64%.
2. Die Zusatzfunktionen des univariaten linearen Analyse-Modells
Das univariate Modell bietet eine Vielzahl an weiteren Analysefunktionen, die über die Buttons A) "Optionen", B) "Geschätzte Randmittel" und C) "Diagramme" auf der Eingangsseite aufzurufen sind.
a) Die Analysefunktionen anfordern
A) Der Aufruf der "Optionen"
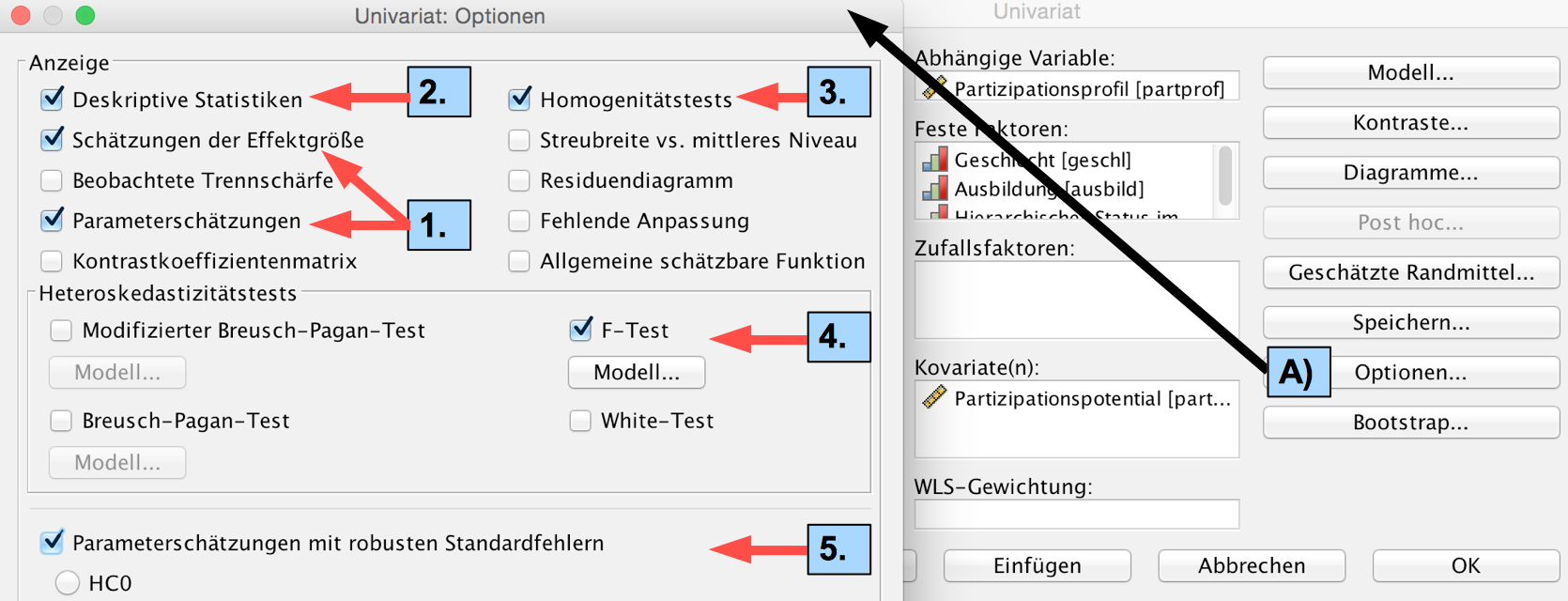
Screenshot 12-55: A) Das Tool "Optionen
Anmerkungen:
zu 1: Die Schätzung der Effekte und der Parameter
In der mehrfaktoriellen Varianzanalyse bezeichnet die Effektgröße einer Komponenten (Faktor bzw. Wechselwirkung) die Auswirkung dieser Komponenten auf die abhängige Variable. Sie wird über das "partielle" eta-Quadrat der Komponente gemessen (vgl. dazu Punkt b).
Im Modul "Konzepte und Definitionen" hatten wir gesehen, wie sich die Faktoren und ihre Wechselwirkungen in Dummy- bzw. (0,1)-Variablen umwandeln lassen, um sie für eine Regressions-und Korrelationsanalyse zu erschießen. Die Schätzung der Parameter der Regressionsfunktion wird in Punkt c) diskutiert.
zu 2 u. 3: Die Analyse der Zellen-Mittelwerte und -Streuungen (vgl. Punkt d)
Mit den "deskriptiven Statistiken" werden die Mittelwerte und die Standardabweichungen der Zellen abgerufen.
Mit dem "Homogenitätstest" wird der Levene-Test auf Homogenität der Zell-Varianzen angefordert.
zu 4 und 5: Heteroskedastizitätstests und Parameterschätzungen mit robusten Standardfehlern (vgl. Punkt d)
Mit dem F-Test werden die Zellvarianzen auf Heteroskedastizität (Abhängigkeit der Varianzen von den Faktorstufen) untersucht.
Entsprechen die Annahmen über die Varianzen nicht den gegebenen Daten, können anstelle der unter 1) geforderten Parameterschätzungen robuste Schätzungen durchgeführt werden.
B) und C) Der Aufruf der "Geschätzten Randmittel" und der "Diagramme"
Screenshot 12-56: Die Tools B) "Geschätzte Randmittel" und C) "Diagramme"

Anmerkungen:
zu B: Geschätzte Randmittel (vgl. Punkt e)
Die geschätzten Randmittel sind die, aus den Regressionsfunktionen zu erwartenden Mittelwerte für die Faktorstufen.
zu C: Diagramme (vgl. Punkt e)
Mit den Profilplots werden die geschätzten Randmittel (analog zu den Mittewertdiagrammen der einfaktoriellen Varianzanalyse) grafisch dargestellt.
b) Die Schätzung der Effekte
Der Schätzung der Effekte im Rechenbeispiel liegt das mehrfaktorielle angepasste (vgl. Abschnitt b) und das hierarchische Modell (vgl. Abschnitt c) zugrunde. Die Ergebnisse finden sich in den letzten Spalten der Screenshots 12-51 und 12-52.
Die Definition der "partiellen" eta-Quadrate (Effekte)
Die eta-Quadrate der Komponenten drücken die Anteile der Komponenten an der Erklärungskraft des Modells aus. Von SPSS wird der Beitrag einer Komponenten (deren Quadratsumme) nicht wie bei den bisherigen Definitionen von R2 und η2j auf die Quadratsumme des Modells bezogen, d.h. auf die korrigierte Gesamtvariation (bisher als SAQ-gesamt bezeichnet), sondern mit den "partiellen" Eta-Quadraten η2p auf die "Gesamt"-Variation, die unabhängig von den Effekten der anderen Komponenten ist. Hier sind beide Formeln einander gegenübergestellt:

Die Modifikation der Formel bewirkt, dass der Nenner die Beiträge der anderen Komponenten nicht mehr enthält und deshalb kleiner ausfällt als im traditionell berechneten Maß.
Aus diesem Grund liegen die "partiellen" Eta-Quadrate über den Eta-Quadraten (vgl. die Spalten 3 u. 4, Tab. 12-6 und Tab. 12-7).
Die Komponentenbeiträge und die Effekte im gesättigten und im hierarchischen Modell
Tabelle 12-6: Die Erklärungsbeiträge und Effekte der Komponenten im gesättigten Modell
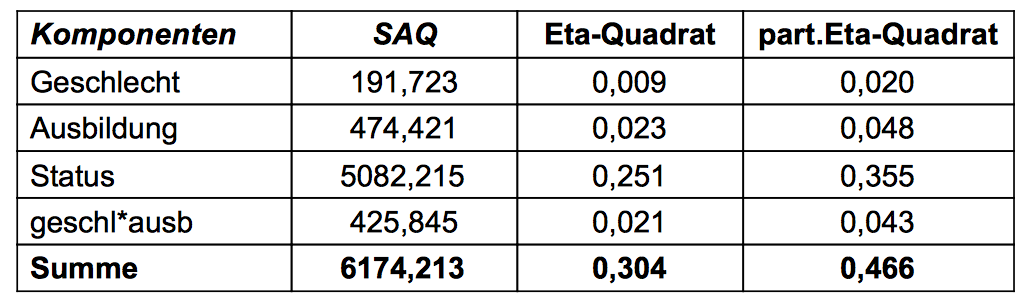
Bei einer Fehler-Quadratsumme von 9403,4 und einer erklärten Quadratsumme von 10871,7 (vgl. Screenshot 12-51 bzw 12-52) ergibt sich für den Faktor Status ein Betrag von η2j = 0,251 = 5082,2 / (10871,7 + 9403,4). Für das "partielle" Eta-Quadrate ergibt sich η2p = 0,355 = 5082,2 / (5082,2 + 9403,4).
Im gesättigten Modell addieren sich weder die Eta-Quadrate der Komponenten noch die "partiellen" Eta-Quadrate zum Eta-Quadrat des Gesamtmodells von 0,536. Durch die Überschätzung der "partiellen" Eta-Quadrate im modifizierten Berechnungsverfahren summieren sie sich immerhin auf eine Betrag von 0,466 auf.
Tabelle 12-7: Die Erklärungsbeiträge und Effekte der Komponenten im hierarchischen Modell

Berechnet man die Eta-Quadrate im hierarchischen Modell nach dem herkömmlichen Verfahren, fallen sie kleiner aus als die "partiellen", addieren sich allerdings zum eta-Quadrat des Gesamtmodells, wohingegen die Summe der "partiellen" Eta-Quadrate den gesamten Erklärungs-Betrag deutlich übertrifft (vgl. Tab. 12-6 u. 7, Summenzeile).
Fazit:
Im angepassten Modell wird die Gesamterklärungskraft des Modells nicht auf die Komponenten aufgeteilt, damit sind deren Effekte über η2j nicht bestimmbar. Ob dies mit dem Konzept der "partiellen" Eta-Quadrate η2p angemessen erfolgt, ist allerdings fraglich.
Eine m.E. sach- und formallogische Lösung bietet das hierarchischen Modell mit der traditionellen Ermittlung der Beiträge über die Eta-Quadrate, die - nebenbei gesagt- als Eta-Quadrate von Partialvariablen die eigentlichen partiellen Eta-Quadrate sind.
Diese addieren sich korrekterweise im hierarchischen Modell zum R-Quadrat des Gesamtmodells auf.
Allerdings müssen die korrekten Eta-Quadrate der Komponenten per Hand berechnet werden.
c) Die Schätzung der Parameter
Die Parameterstruktur
Im Modul "Konzepte und Definitionen" hatten wir gesehen, wie sich die Faktoren und ihre Wechselwirkungen in Dummy- / (0,1)-Variablen umwandeln lassen, um sie für eine Regressions-und Korrelationsanalyse zu erschießen.
Dazu werden bei k Faktorstufen k-1 Dummy-Variablen gebildet. Wir erhalten also:
für den Faktor "Geschlecht" (mit k = 2) die Variable B1,
für den Faktor "Ausbildung"(mit k = 6) die Variablen C1....C5,
für den Faktor "Status" (mit k = 7) die Variablen D1....D6 sowie
für die Wechselwirkungen "geschl*ausbild" die Variablen W1....W11.
Die Regressionsfunktion in der mehrfaktoriellen Varianzanalyse
Der Funktionswert xjklc stellt den geschätzen Mittelwert der abhängigen Variablen X in der Zelle j,k,l dar.
Die Funktion lautet dann in ausführlicher Schreibweise:
xjklc = a* + b1* · B1 + c1* · C1 + .... + c5* · C5 + d1* · D1 + .... + d6* · D6 + w1* ·W1 + .... + w11* ·W11
Da je nach Faktorausprägung viele der dichotomen Variablen den Wert "0" annehmen, liegt es nahe, diese Komponenten in einer verkürzten Fassung zu eliminieren und nur noch die Komponenten aufzuführen, deren Variablenwert "1" beträgt, der explizit ebenfalls nicht mehr notiert werden muss. Damit besteht die Funktion nur noch aus den Regressionsparametern:
xjklc = a* + bj* + ck* + dl* + wm*+ .... + wr*
Die partiellen Regressionsparameter anfordern
Die partiellen Regressionsparameter werden über "Optionen" (vgl. Screenshot 12- 55) angefordert.
Die Tabelle der geschätzten Regressionsparameter
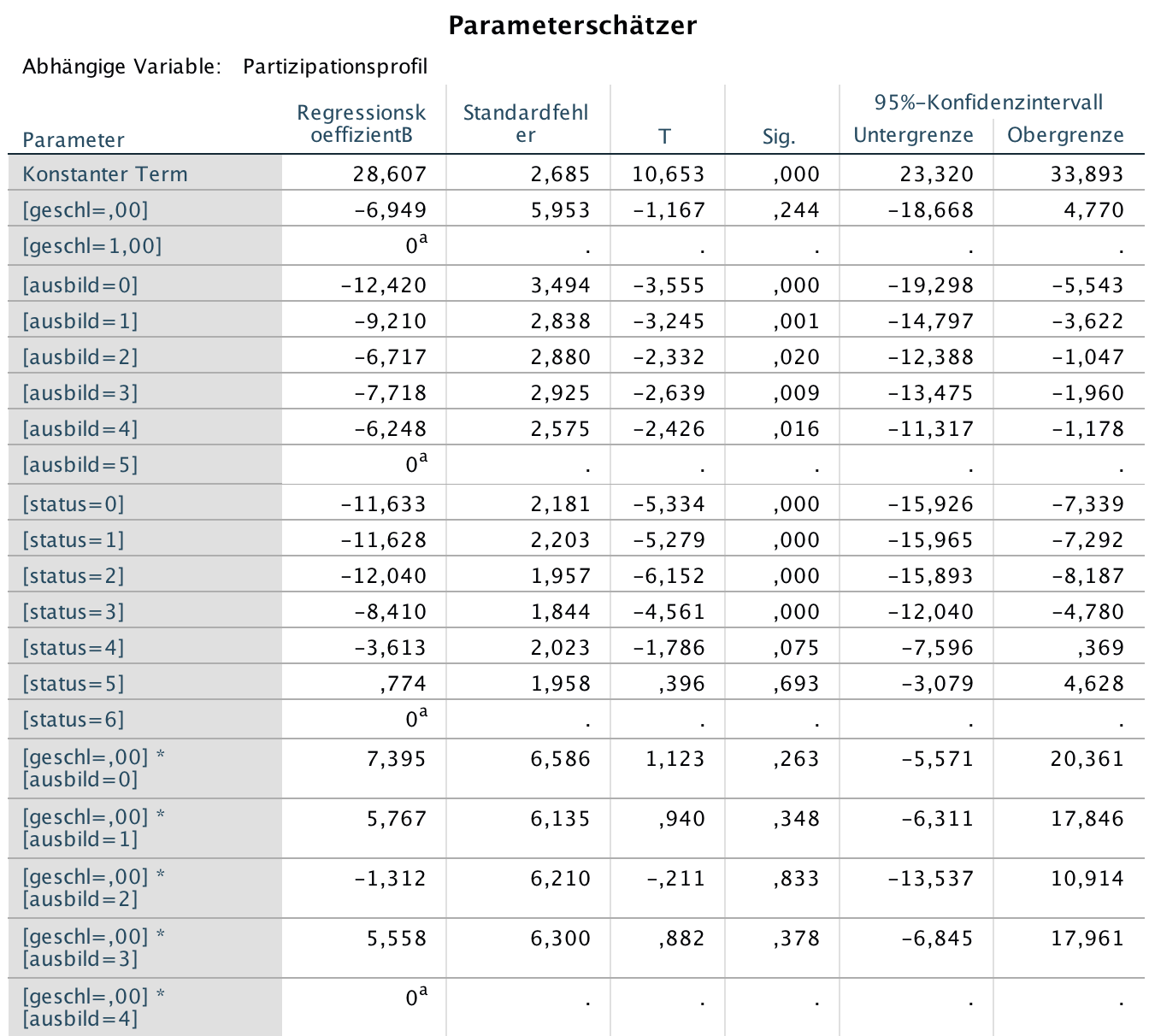
Screenshot 12-57: Die Parameterschätzer
Anmerkungen:
Die Darstellung der Tabelle wurden aus Platzgründen gekürzt. Die fehlenden letzten sechs Zeilen beinhalten jeweils Parameter mit Werten von "Null".
Die Parameterschätzer sind für die beiden unter 1. b) und c) vorgestellten Modelle identisch.
Die Interpretation des Ergebnisses
-
Der konstante Term wird in x1c realisiert, wenn in allen Komponenten die höchste Faktorstufe gegeben ist.
Für "geschl = 0" (d.h. "w") reduziert sich der Wert von x1c gegenüber der Konstanten um den Betrag von 6,949.
Gilt weiter "ausbild = 2" erfolgt eine weitere Reduktion um 6,717.
Ein Status von "4" mindert den Variablenwert um
3,613 usw.
Der geschätzte (Durchschnitts-)Wert der Faktorkombination (Geschlecht = 0, Ausbildung = 2 und Status = 4)
ergibt sich dann einschließlich der Wechselwirkungen als x1c = 28,607 - 6,949 - 6,717 - 3,613 - 1,312 = 10,016.
Aus dem Vergleich der Regressionskoeffizienten eines Faktors kann ausserdem unmittelbar auf die Effekte der Faktorstufen geschlossen werden.
d) Die Analyse der Zell-Mittelwerte und -Streuungen
Zur Vereinfachung der Präsentation werden diese SPSS-Tools anhand einer zweifaktoriellen Analyse unter Berücksichtigung der Faktoren Ausbildung und Status sowie ihrer Wechselwirkung vorgestellt.
Die Anforderung der Tabelle und des Tests (vgl. Screenshot 12-55)
Die Zellen-Mittelwerten und -Streuungen werden unter der "Optionen - Deskriptive Statistiken",
die Prüfung der Homogenität der Zell-Varianzen wird unter "Homogenitätstest" angefordert.
Die Präsentation der deskriptiven Zellenstatistiken
Wegen der Anzahle der Zellen und des Umfangs der Tabelle werden nur Zellen der Statuskategorien bis einschl. Teamleiter gezeigt.
|
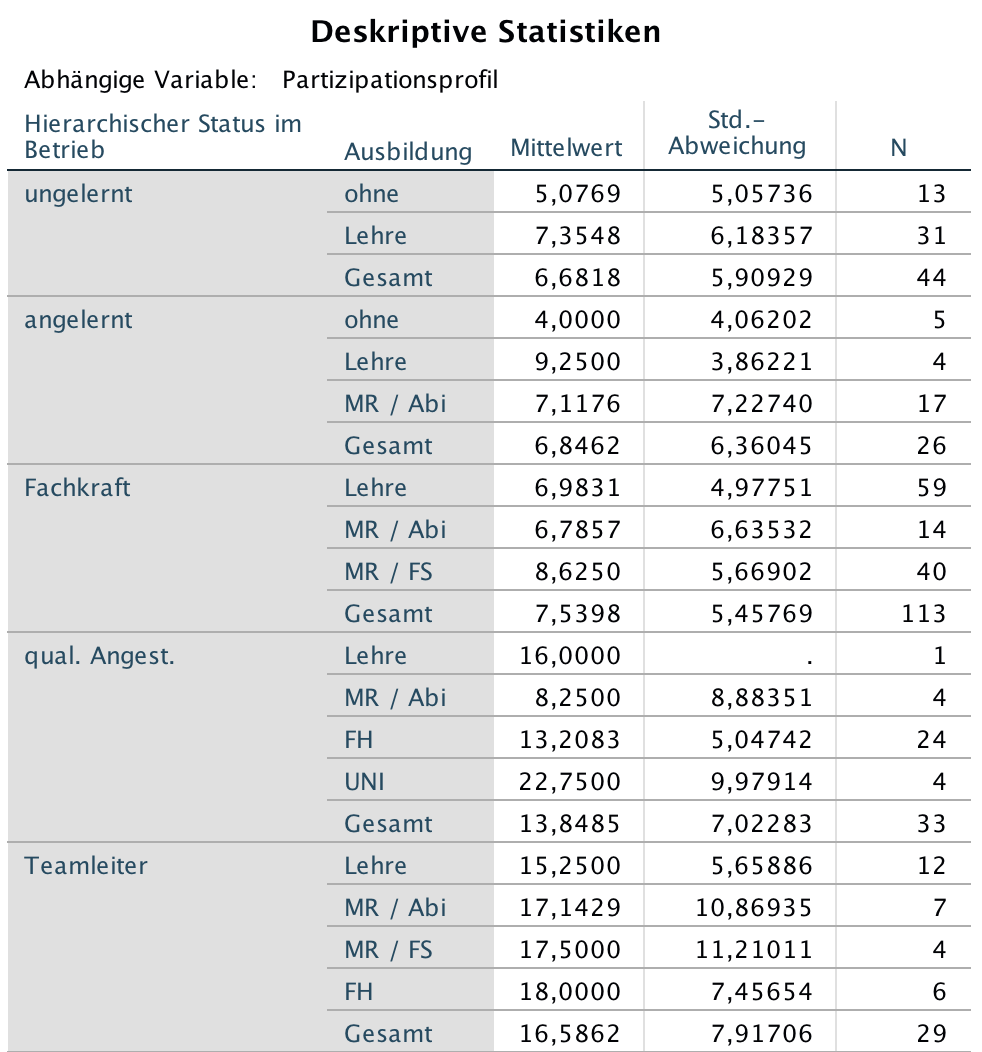
Screenshot 12-58: Die deskriptiven Statistiken (Auszug)
|
|
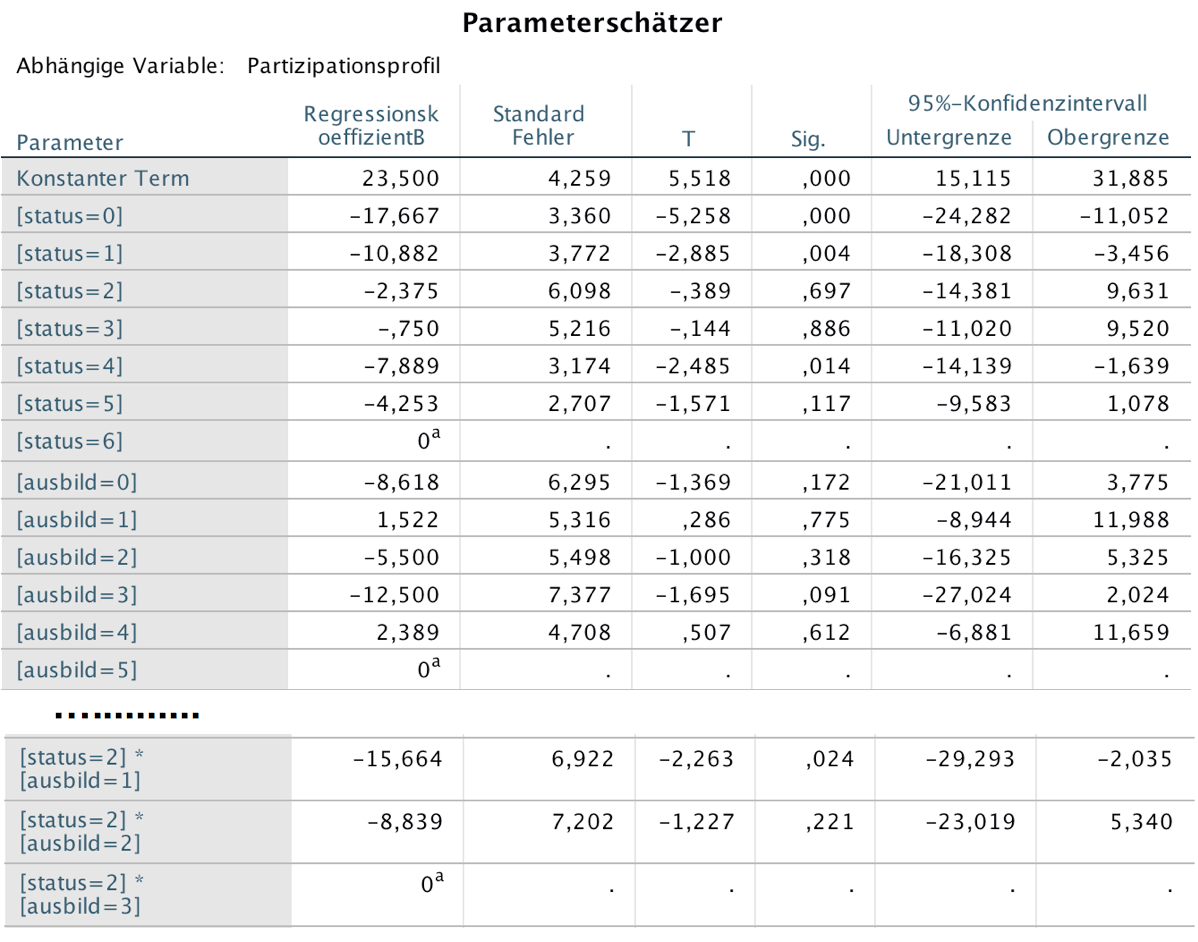
Screenshot 12-59: Die Parameterschätzungen für das Modell (Auszug zur Berechnung der Randmittel, vgl Punkt e).
|
|
|
Anmerkungen:
Die Mittelwerte der Beteiligung der einzelnen Ausbildungs- und Statusgruppen an den Entscheidungsprozessen unterscheiden sich deutlich mit einem Wert von 4 - 5 für die ausbildungs- und status-niedrigsten Gruppen und von etwa 25 für die höchsten (im Auszug nicht enthalten).
Die ausgewiesenen Standardabweichungen in den Zellen liegen zwischen etwa 4 und 11.
Diese Ergebnis war aufgrund der geringen Anzahl von Fällen in einigen Zellen zu erwarten.
Die Homogenität der Varianzen ist allerdings eine Voraussetzung für die Zuverlässigkeit der Testergebnisse. Deshalb ist ein Levene-Test auf Varianzenhomogenität sinnvoll:
Screenshot 12-60: Der Test auf Homogenität der Varianzen
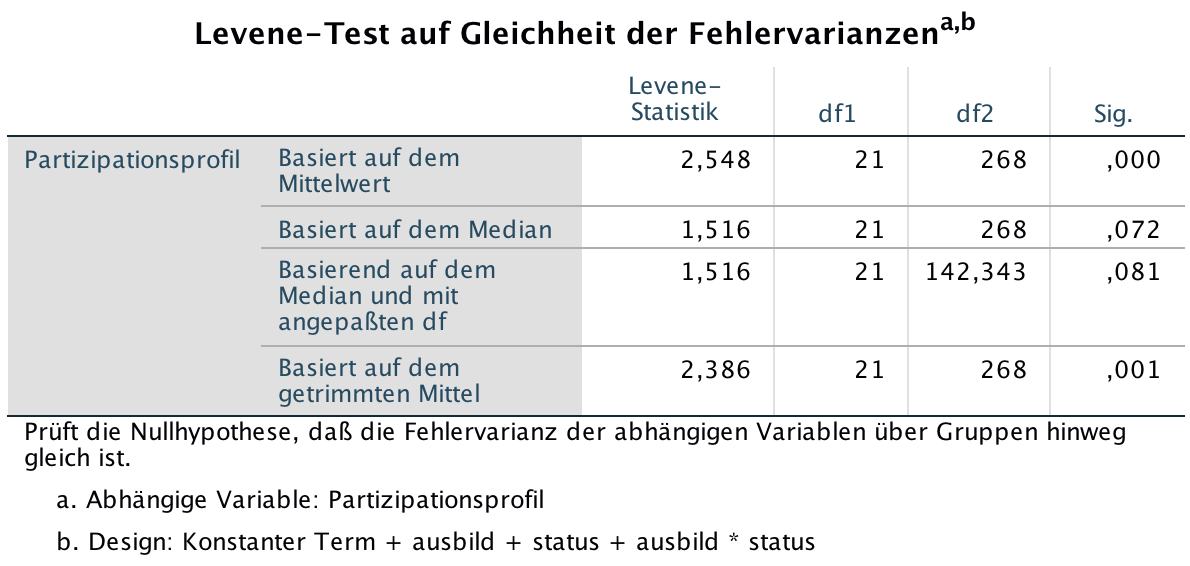
Anmerkungen:
Bei einer Signifikanz < 0,01 muss die Hypothese, die Varianzen in den Gruppen seien nur zufällig unterschiedlich, zurückgewiesen werden.
Je nach Testbasis (Mittelwert, Median oder getrimmtes Mittel) kann die Null-Hypothese gerade noch oder nicht zurückgewiesen werden.
Sicherheitshalber sind in diesem Fall robuste Parameterschätzungen (vgl. Optionen) anzuraten.
e) Die Tabellen und Grafiken zu den geschätzten Randmittel
Vorbemerkung
Die geschätzten Randmittel der Faktoren stellen den für die einzelnen Faktorstufen zu erwartenden Durchschnittswert der abhängigen Variablen dar.
Sie werden in SPSS über "geschätzte Randmittel..." als Tabelle und über "Diagramm..." als Grafik angefordert (vgl. Screenshot 12-56).
Zur Vereinfachung der Präsentation werden diese SPSS-Tools anhand einer zweifaktoriellen Analyse unter Berücksichtigung der Faktoren Ausbildung und Status sowie ihrer Wechselwirkung ausgeführt.
Das Konzept der geschätzten Randmittel
Um das Konzept der geschätzten Randmittel nachvollziehen zu können, ist es hilfreich diese auf die empirischen Randmittel zu beziehen.
Die empirischen Randmittel einer mehrfaktoriellen Analyse sind die Mittelwerte der abhängigen Variablen in den einzelnen Faktorstufen der einbezogenen Faktoren.
In der einfaktoriellen Analyse werden sie im Mittelwertdiagramm grafisch veranschaulicht, in der zweifaktoriellen Analyse finden sie sich als Spalten- und Zeilenmittel (vgl. Tabelle 12-5 im vorangegangenen Modul "Definitionen und Konzept").
Beispieldaten für die einzelnen Faktorstufen des Faktors "Status" sind im Screenshot 12-58 unter "insgesamt" zu finden. Sie ergeben sich allgemein als gewogenes Mittel der Zellmittelwerte und z.B. für die Faktorstufe "Fachkraft" wie folgt:
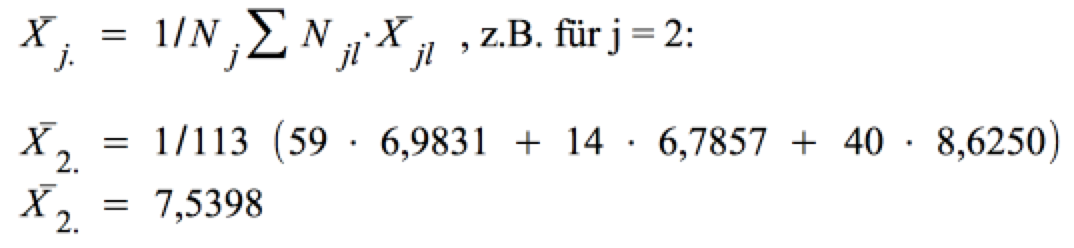
Die Formel für die geschätzten Randmittel nimmt nun gegenüber der obigen Formel zwei wesentlich Veränderungen vor:
Zum einen bezieht sie sich nicht auf die empirischen Zellmittelwerte sondern auf die über die varianzanalytische Regressionsfunktion (vgl. die Regressions-Funktion in Punkt c) geschätzten Zell-Mittelwerte x1c und bindet damit den analytischen Erkenntnisgewinn in die Berechnung ein.
Zum anderen werden die Gewichte Njl = 1 gesetzt, um Zufälligkeiten der Zellenbesetzung zu eliminieren.
Daraus resultiert die Formel:
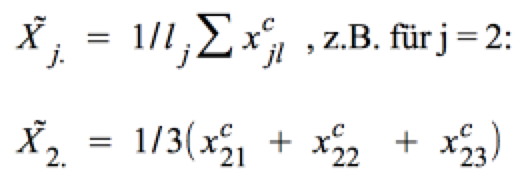
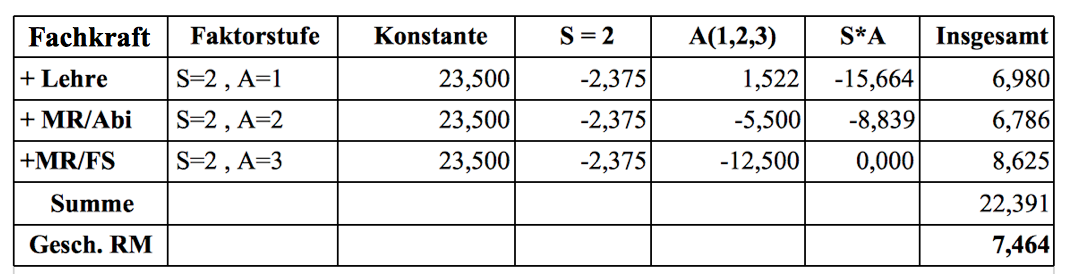
Ein Rechenbeispiel: Unter Verwendung der Parameterschätzer aus Screenshot 12-59 ergibt sich für die Faktorstufe 2 des Faktors "Status" ein geschätztes Randmittel von 7,464:
Tabelle 12-8: Berechnung des geschätzten Randmittels der Faktorstufe "Status=Fachkraft"
Die Tabellen der geschätzten Randmittel
|
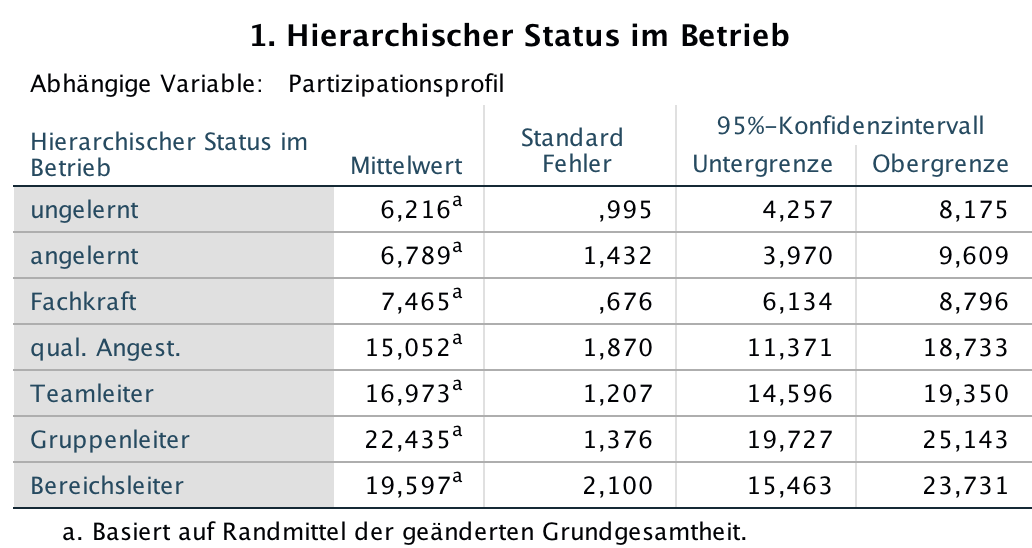
Screenshot 12-61: Die geschätzten Randmittel des Faktors "Status"
|
|
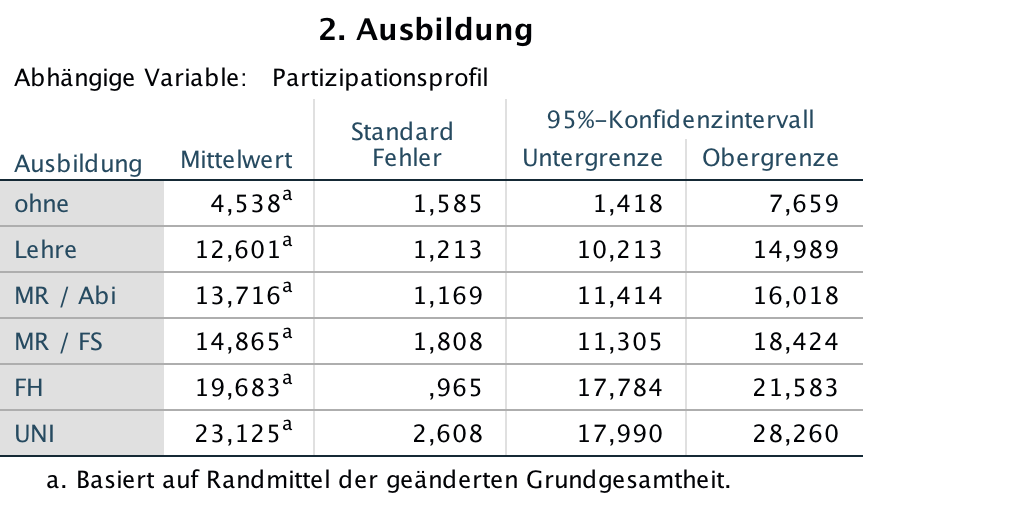
Screenshot 12-62: Die geschätzten Randmittel des Faktors "Ausbildung"
|
|
|
Die Profil-Diagramme der Faktoren
|
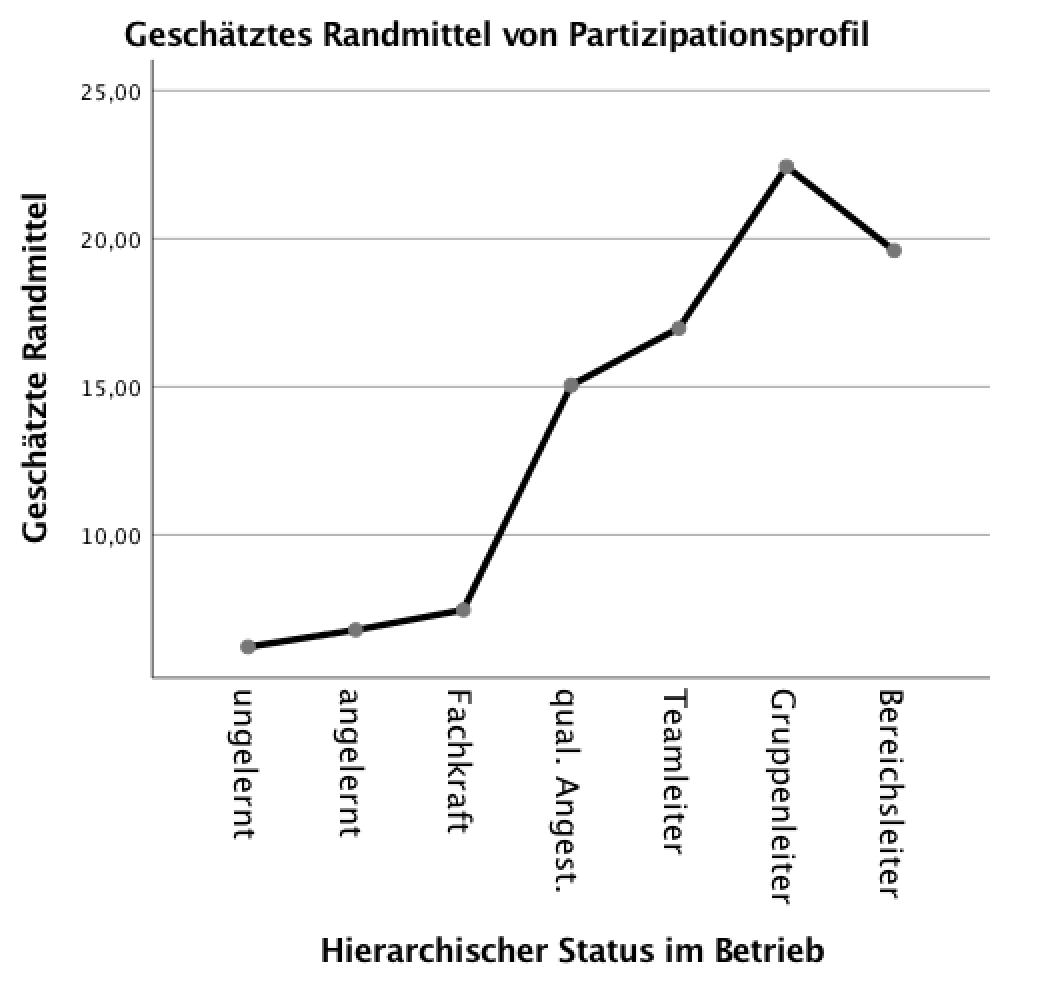
Screenshot 12-63: Das Profildiagramm des Faktors "Status"
|
|
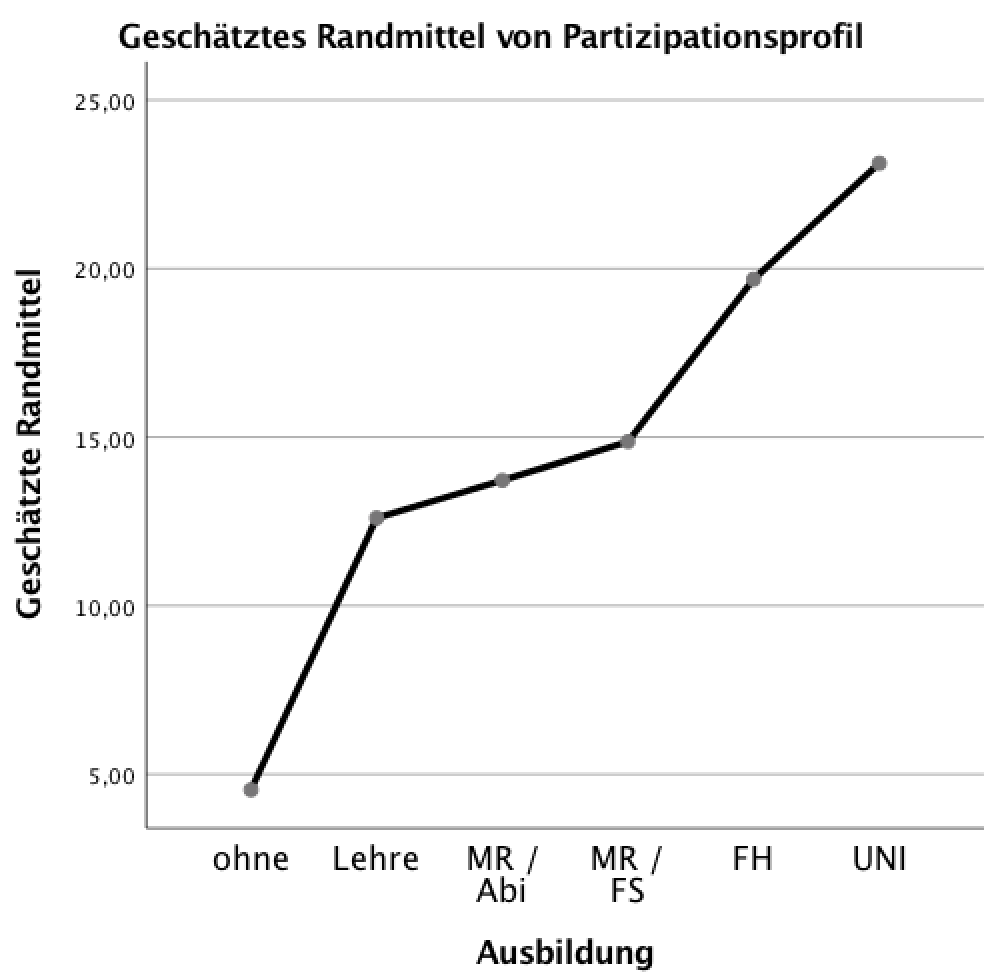
Screenshot 12-64: Das Profildiagramm des Faktors "Ausbildung"
|
|
|
Der Vergleich der geschätzten mit den empirischen Randmitteln
Zum Vergleich werden die bereits in der einfaktoriellen Varianzanalyse präsentierten empirischen Randmittel hier noch einmal zitiert:
Screenshot 12-65: Die empirischen Randmittel der Faktoren "Ausbildung" und "Status"
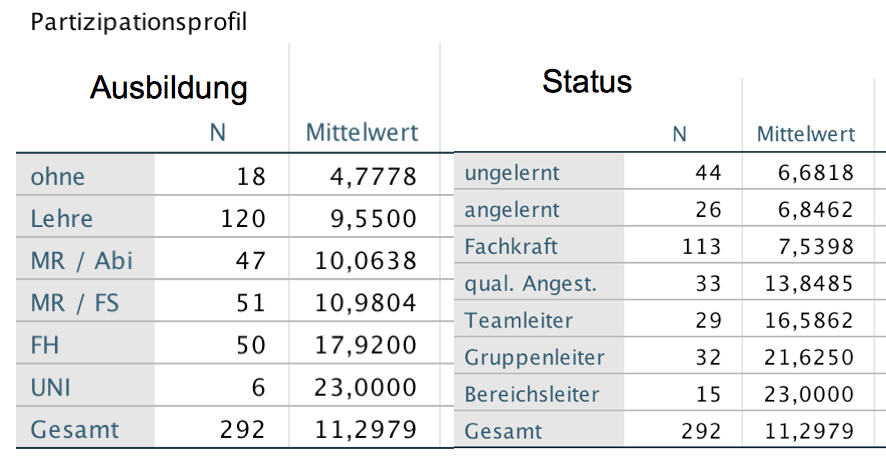
Für die Ausbildung zeigt sich im Vergleich zum Screenshots 12-62, dass die mehrfaktoriellen Analyseergebnisse i. A. für alle Ausbildungsstufen (abgesehen von der niedrigsten) eine z.T. deutlich stärkere Beteiligung erwarten lassen als im konkreten betrieblichen Fall.
Bezüglich des Status gilt hingegen, dass die Beteiligung der unteren Positionen an den Entscheidungsprozessen geringer und die der oberen Positionen etwas höher eingeschätzt wird. Davon ausgenommen ist die geschätzte Beteiligung in der höchsten Statusposition, die deutlich geringer zu erwarten ist.
Anmerkung:
.
Das Testverfahren für die Komponenten findet sich in
ViLeS 2, Modul "Test der Regressions- und Korrelationskoeffizienten, Teil C Die Tests der η2-Koeffizienten in der ein- und mehrfaktoriellen Varianzanalyse"
3. Aufgaben
Die Beispielsrechnungen haben gezeigt, dass die vielfältigen Aspekte einer mehrfaktoriellen Varianz- Kovariaznanalyse mit den Tools des "Allgemeinen linearen Modells - Univariat..." " angesprochen werden können. Dabei wird empfohlen in der Bearbeitung der Aufgaben verschieden Modelle einzusetzen.
a) Die Analyse der gewünschten Beteiligung (Variable partpot)
Zum Vergleich mit den obigen Beispielsrechnungen soll nun unter Verwendung der Datei Partizipation_1.sav mit SPSS der Zusammenhang zwischen der gewünschten Beteiligung und den gerade eingesetzten Faktoren sowie der, diesmal als Kovariate fungierenden Variablen "Partizipationsprofil" untersucht werden.
b) Die Aufgabenstellung
Ermitteln und kommentieren Sie bei Ihren Analysen der verschiedenen Modelle die folgenden Komponenten:
die ANOVA-Tabelle und das Maß zur Stärke des Zusammenhangs für
Die Tabelle der deskriptiven Statistiken und
den Homogenitätstest für die Zellvarianzen.
Schätzen Sie die Effekte und die Parameter.
Erzeugen Sie die Tabellen und Grafiken zu den geschätzten Randmitteln.
|